SRM 549 div1 easy: PointyWizardHats

問題

TopCoder Statistics - Problem Statement

円錐のセットを 2 つ用意する。2 つのセット Top, Bottom は次のように使う。

• Top の円錐を Bottom の円錐の上にかぶせるように乗せる。

ここで, Top の円錐の半径は Bottom の円錐の半径より小さくなければならない。また, Top の円錐の頂点が Bottom の円錐の頂点に乗る感じになってはならない(解説の図参照)。

これを満たすようにマッチングを取っていくとき, マッチングの最大値はいくつになるか。

解法

最大マッチング問題なので, 最大流に帰着できます。後は, そのグラフを作るのが問題です。

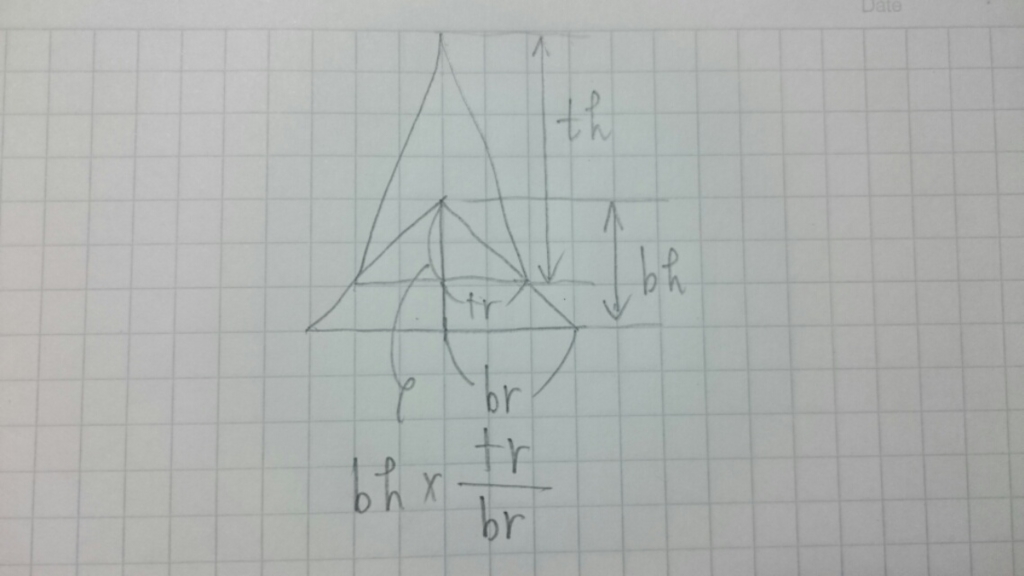
Bottom グループの円錐の半径を br, 高さを bh, Top グループの円錐の半径を tr, 高さを th とするとき, 写真のようになっていればよいのですが, この条件は

th > bh*tr/br

と書き表せるので, この条件を満たすものについてだけ辺を張ってグラフを作りましょう。

bool ok(int th, int tr, int bh, int br) {
    if (tr >= br) return false;
    return bh*tr < th*br;
}

class PointyWizardHats {
public:
    int getNumHats(vector <int> topHeight, vector <int> topRadius, vector <int> bottomHeight, vector <int> bottomRadius) {
        int n = topRadius.size(), m = bottomRadius.size();
        int s = n+m, t = s+1, V = t+1;
        Dinic dinic(V);
        for (int i = 0; i < n; i++)
            dinic.add_edge(s, i, 1);
        for (int i = 0; i < m; i++)
            dinic.add_edge(i+n, t, 1);
        for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) {
            if (ok(topHeight[i], topRadius[i], bottomHeight[j], bottomRadius[j])) {
                dinic.add_edge(i, j+n, 1);
            }
        }
        return dinic.max_flow(s, t);
    }