AOJ 2638 Hyperrectangle

問題

Hyperrectangle | Aizu Online Judge

解法

まず, このページを見ると d 次元の立体における体積の求め方が分かります。各辺の長さが 1 の三角錐(?) の体積は 1/d! なんですね。
単体 (数学) - Wikipedia

で, 後は包除原理です。例えば 各辺の長さが {2, 3, 5}, S = 9 の場合を考えます。このとき,

• 普通に全体を考えると 9^3 / 6 の体積を持つ
• これだと余計に体積を考えているので体積を間引く。はみ出ているものとして,
  • 一辺が 9-2 = 7 の正三角錐
  • 一辺が 9-3 = 6 の正三角錐
  • 一辺が 9-5 = 4 の正三角錐
• これだと引きすぎているので体積を足す。はみ出ているものとして,
  • 一辺が 9-2-3 = 4 の正三角錐
  • 一辺が 9-2-5 = 2 の正三角錐
  • 一辺が 9-3-5 = 1 の正三角錐

3 次元の図を上から見るとこんな感じです。もうちょっと足し匹するグループがありますがイメージは分かると思います。

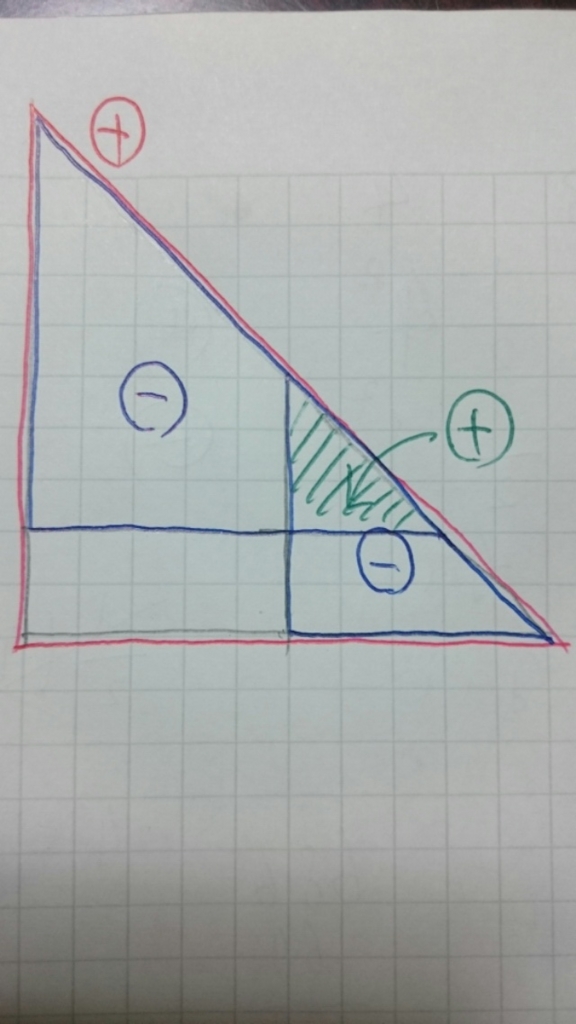
普通に包除原理をすると O(2^d) かかりますが, 今回の包除原理は足し引き以外重要でないので, 「S から辺の長さをいくつ引いたか」の偶奇のみを覚えておけば良いです。つまり,

dp[d][rest][flag] = (d 番目の時点で, 残りの単体の辺の長さは rest で, S から辺を引いた回数の偶奇は flag であるときの体積) というような dp をやります。この考え方は過去の TC med にあったような気がします。
mayokoex.hatenablog.com

const int MAXD = 303;
const int MOD = 1e9+7;
int D, S;
int l[MAXD];
int dp[MAXD][MAXD*MAXD][2];

ll mod_pow(ll x, ll p, int MOD) {
	if (x == 0) return 0;
    ll a = 1;
    while (p) {
        if (p%2) a = a*x%MOD;
        x = x*x%MOD;
        p/=2;
    }
    return a;
}

int dfs(int d, int rest, int flag) {
	int& ret = dp[d][rest][flag];
	if (ret >= 0) return ret;
	if (d == D) {
		ret = mod_pow(rest, D, MOD);
		if (flag) ret = -ret;
		ret = (ret%MOD+MOD)%MOD;
	} else {
		ret = dfs(d+1, rest, flag);
		if (rest >= l[d]) {
			ret += dfs(d+1, rest-l[d], flag^1);
		}
		ret %= MOD;
	}

	return ret;
}

int main() {
    cin.tie(0);
    ios::sync_with_stdio(false);
	cin >> D;
	for (int i = 0; i < D; i++)
		cin >> l[i];
	cin >> S;
	memset(dp, -1, sizeof(dp));
	cout << dfs(0, S, 0) << endl;
    return 0;
}