todolist 作りました
todolist 作ったので報告だけしておきます。
https://mayoko-todolist.herokuapp.com/
まだ色々と機能追加するつもりです。今 todoist ってアプリ使ってるけどこの todolist で完結できるようになったらいいなー
読んでいる英語の本
みなさん英語の勉強していますか?僕はしています
英語の学習の上では多読も大事っぽいです。下のサイトにもそう書いてある。
mutuno.o.oo7.jp
と言うことでなんか英語で本を読みたいわけですが, どう言う本を読めばいいのかがわからないのが困りどころです。
と言うことで, 自分が読んだ本(途中までのも含めて)を紹介して誰かの役に立てばいいなーと思いながら記事を書きます(あと自分のモチベも上がりそう)。
どんどん増やしていきたい。
僕は kindle で読んでますが, kindle だと単語を長押しするだけで辞書が出てくるのでかなり便利です(熟語とかで "put the meeting off" の put off を調べたいときは無理ですがそれでも単語調べる時間は減ります。あと動詞が現在進行形になってたりしても空気読んでくれたりすることもあります)。
漫画
Kiniro Mosaic(English Edition)
https://www.amazon.co.jp/gp/product/B01LYBKDWH/ref=ppx_yo_dt_b_d_asin_title_o07?ie=UTF8&psc=1
きんモザです。これは残念ながら kindle から辞書が引けません。
漫画は結構気楽に読めるし絵があるので雰囲気で何が言いたいのかもわかっていいと思います。あと可愛い。
使われている単語とかは日常単語が多いにも関わらず割と知らなかったりするのが多かったので単語の勉強にもなるし, 最初から本読むのは怖いと言う人にはいいかもしれません。
あと一番後ろについている翻訳 tips も面白いです。
Gabriel Dropout (English Edition)
https://www.amazon.co.jp/gp/product/B0739WKS2F/ref=ppx_yo_dt_b_d_asin_title_o08?ie=UTF8&psc=1
ガブドロです。これも kindle から辞書が引けません。
きんモザとだいたい同じ感想ですが, 特にウクニキアの英語が難しいです。
The Promised Neverland
https://www.amazon.co.jp/gp/product/B0767YW5TY/ref=ppx_yo_dt_b_d_asin_title_o04?ie=UTF8&psc=1
約束のネバーランド英語版です。
たまに難しめの単語がある気がしますが, 基本的にはスイスイ読めます。
僕は原作知らなくて, たまにオススメしてる人がいるなぁ〜と思っている程度だったのですが, 主人公たちの頭脳戦も面白いし, これからどういう展開になるのかもすごく気になります。
読み物
Funny English 1-2-3: Funny Mistakes Japanese Make in English (English Edition)
https://www.amazon.co.jp/exec/obidos/ASIN/B017T5CT4S/atsuo06-22/
日本人がよくする間違いをまとめたものです。Kindle Unlimited で読めます。
例えば, 「面倒くさい」を google 検索すると troublesome が出てくると思いますが(出てこなかったらごめん)これはめっちゃ古臭い表現らしいです, とかそういのがたくさん書いてあります。
30 個の間違いが紹介されていますが, 一つ一つは短いので気楽に読めます。
ただ, たまに挿入される "Haha!" に少しイラっとくることもあります。
途中に練習問題みたいなのがありましたが, それは興味ないので飛ばしました。
Who Moved My Cheese?: An A-Mazing Way to Deal with Change in Your Work and in Your Life
https://www.amazon.co.jp/exec/obidos/ASIN/B004CR6AM4/atsuo06-22/
日本語で「チーズはどこに消えた?」と言うのが出てて, かなり有名な話っぽいですが僕は読んだことなかったです。
自己啓発本に近い気がします。個人的には共感できる考え方でした(実践しているかはともかく)。
自己啓発本と言うと難しい表現がたくさん出てきそうな感じがありますが, この本は例え話(チーズを探し求めるネズミと小人)で話が進むのでそんなに読むのに苦労しませんでした。
English Short Stories For Intermediate Learners: 8 Unconventional Short Stories to Grow Your Vocabulary and Learn English the Fun Way! (English Edition)
https://www.amazon.co.jp/exec/obidos/ASIN/B01GBNFEPA/atsuo06-22/
多読するために生まれてきたような本です。Kindle Unlimited で読めます。
全部で 8 個の小話があって, それぞれの小話はいくつかの chapter にわかれています。
それぞれの chapter ごとにチェックテスト, サマリーが書かれているので置いてけぼりになることがないです。
ただ, 英文が流石に簡単すぎておもんなかったので 2 つ小話読んでやめました。
文章のレベルとしては, 「mayoko はお腹が痛くなった。なので彼はトイレに行った。彼はそこでこれからの人生について考え始めた。」みたいなくらい文章が切断されていて中学レベルの英文法すらなるべく使わないようにしている気がします。
Think Like Einstein: Think Smarter, Creatively Solve Problems, and Sharpen Your Judgment. How to Develop a Logical Approach to Life and Ask the Right Questions (English Edition)
https://www.amazon.co.jp/exec/obidos/ASIN/B0725RDXWW/atsuo06-22/
アインシュタインのように考えるにはどうすればいいかをまとめたものっぽいです。Kindle Unlimited で読めます。
色々と creative thinking するための方法論が書いてあるんですが, 箇条書き風にあれもやろうこれもやろうと言っていて全然まとめる気がなさそうだったので途中で読むのをやめました。
言ってること自体はもっともっぽいですが, 多分賢いみなさんはすでに実践していることが多いと思います。
ラノベ
I've Been Killing Slimes for 300 Years and Maxed Out My Level (English Edition)
https://www.amazon.co.jp/gp/product/B0763KWFJT/ref=ppx_yo_dt_b_d_asin_title_o00?ie=UTF8&psc=1
本のタイトルは「スライム倒して300年、知らないうちにレベルMAXになってました」です。
もともと「オレツエーやるなら美少女の方がよくない?」と思ってた僕にはちょうど良さそうな本でした。
まぁゆーてオレツエー関係なくてのほほんとしてるだけですけどね。
まだ途中ですが漫画と同じノリです。心の声が入っている分より英文読んでる感はあります。
ラノベは読んでて面白いし他にあったら読んでみたいですね
プログラミング系
Head First PHP & MySQL: A Brain-Friendly Guide
https://www.amazon.co.jp/gp/product/B00CB30Y2S/ref=ppx_yo_dt_b_d_asin_title_o06?ie=UTF8&psc=1
PHP と MySQL 使って Web アプリケーションを作ろう!って本です。
HTML の雰囲気わかってて if 文 for 文わかりますだったら多分普通に読めます。
ページ数はすごく多いですが挿絵が頻繁に挟まっているので読みやすいです。
あと雰囲気ふざけてるのでそういうのが好きな人は好きだと思います。
参考文献
まとめ
- かぐや様は告らせたいはいいぞ!
畳み込みニューラルネットワークを使って質感を学習してみた
背景
世の中の物質は様々な材質をしており, その材質により物の見え方は大きく異なります。たとえば, アルミニウムなどの金属を見ると光沢感があるように感じると思いますが, 布はそのような光沢感を感じません。今回は, この物体の見え方の意味での質感を機械に学習させて, 「質感 A と質感 B は, 感覚的に(人の直感的に)どれくらい異なるか」ということを学習させることを目標にします。
下の絵は質感の違いの例です。右側の物体は光沢感があって, 中央, 左の物体は光沢感はないですが白黒の違いがあります。

質感の違いを計算出来ると, 質感のデザインを行う際に, 今デザインしている質感と目標の質感がどれくらい異なるのかを数値化できたり, さらに応用すると自分が使いたい質感のデザインを直感的に選択したり(色の選択については, HSV 色空間を使って直感的に出来るようになっていると思いますが, それを質感でも出来るようになる)出来るかもしれません。これを機械学習的にやってみようかなと思ったのがこの記事です。
質感の違いを測る
まず質感の違いをどう測るのかを考えます。何となくの直感ですが, 人はものをパッと見るだけで質感がどんな感じなのかを推測することが出来ると思います。そこで今回はいろいろな質感の画像を作って, 被験者が画像の「似てる・似てない」を判定することで学習データを作ります。
ということで, 考えることは「質感の画像をどう作るか」と「質感の画像をどのように比べて似てる・似てないのデータを作るか」「データからどのように学習するか」の 3 つです。
質感の画像生成
実は質感が決まってもまだものがどう見えるかは決定しません。対象がどう見えるかは, 対象の形, 環境光, そして質感が必要となります。今回は(かなりサボって)これらのうち主に質感のみしか変化させず, 形と環境光はほぼ fix して画像を生成していきます。*1ただ, 形に関しては少し変えます。
画像は BRDF Explorer というものを使って生成しました。また, 質感のデータは MERL BRDF Database を用いました。
https://www.disneyanimation.com/technology/brdf.html
https://www.merl.com/brdf/
下の画像は生成した画像の一例です。コンピュータービジョン的な研究をやってる人ならおなじみだと思いますが, 形状は armadillo です(環境光も論文でよく見るやつだと思いますが名前を知りません, にわかなので)。

質感の画像比較
質感の画像比較に関しては, 過去に似たような研究がなされていたので, それを参考にしました。
Toward a perceptual space for gloss
この論文では, 被験者に対して 3 枚の質感画像を見せます。そして, 「中央の写真に左右どちらの写真の質感が似ていると思うか?」を質問し, 被験者に答えてもらいます。
今回の場合もこれに倣って, この実験を繰り返し行ってデータを作ります。20 代の男性 1 名が実験に参加しましたが, 被験者が苦痛を訴えたので, 比較データはだいたい 400 個しかありません。
学習手法
学習に関して何も知識がないので, 割と適当です。「ネットワークこういう風にした方が良い」とかあったら教えてほしいです。
自分の作ったネットワークは,
- A: 画像を低次元のベクトルにする(今回は可視化がしたかったので 2 次元)畳み込みネットワーク
- B: 低次元のベクトル同士の距離を計算することで, 「似てる・似てない」を計算する層
の 2 つに分かれています。各被験者実験データは 3 枚の画像から構成されていますが, まず 3 枚の画像それぞれを A のネットワークに入れて低次元ベクトルにし, それを B のネットワーク(?)に入れて「被験者が『左の方が近い』と答える確率はこうだよ」ということを計算します。
1 つ目のネットワークは, VGG16 を単純化したものを使いました。VGG16 を参考にした理由は, どっかの話で「VGG16 でスタイル変換が出来るよ」という話を聞いたからで, これを用いると(質感とスタイルは似てるところがあるので)質感を計測したい対象の形が変わってももある程度正確に質感の違いを予測できるのではないかと考えたからです。
普通の VGG16 では 1000 クラス分類をしてますが今回は上で書いた通り 2 次元ベクトル化したいだけなので出力ベクトルは 2 次元です。
2 つ目のネットワーク(?)では, 低次元化したベクトルに関して, 左画像と中央画像のベクトルの距離を d_L, 右画像と中央画像のベクトルの距離を d_R とし, 1 / (1 + exp(d_L - d_R)) を計算することで, 被験者が左と答えるか右と答えるかをモデル化しました。
一応コードも置いておきます。Google Colaboratory で実装しました。
BrdfNetwork.ipynb - Google ドライブ
実験結果
上記のような方針で実験を行った際の, 質感の二次元分布を示します。
まず armadillo オンリーで実験を行った場合ですが, この場合は結構いい感じに分布してる気がします。傾向として, 右側に白色が, 左上側に黒色が分布しており, かつ下側の光沢感が強い傾向が読み取れます。

次に, sphere と armadillo を混ぜた場合の結果です。うーむ。何となく分かれてる気がする。

bunny と armadillo です。大きく見ると分かれてる感がありますが細かく見ると一か所にいろんな質感(白黒)があってダメな感じがします。

まとめ
- 質感の違いをニューラルネットワークを使って学習してみた
- 形が 1 種類の時は結構いい感じに分布している
- 形が増えるとイマイチだけどそもそも学習データ少ないからかもしれない
- Persona 5 と大神は良かったぞ
ISUCON 8 予選に参加しました
ISUCON8 の予選に参加しました。
詳しい記事は我らがリーダー(?)が書いています
brookbach.com
とりあえず僕も書くかっていうだけ書いておきます。
今回は"前半戦は"座るだけではなかったので良かった(多分一番おいしいところを持っていった)
本番の流れ
僕はサーバーの設定ファイルとかよくわからない(えぇ…)のでそこらへんは任せて最初からアプリの実装を見たりデータベースの仕様を確認したりしていました。
で, get_event 関数がクソ遅そうだったのでそれの報告と改善方法を言ったら「やって~」と言われたので実装
実装内容
- 各 sheet 毎に SQL を呼び出しているのが遅そうなので一回のクエリですべての情報を引き出すように変更
- 具体的には SELECT * FROM reservations WHERE event_id = ${id} みたいな感じのクエリを呼び出せば, イベントごとの sheet 情報が引き出せる
- sheet 情報は固定なので "ベタ書き"(???)
okeigo 君が開発用サーバーも用意してくれてたのでそっちでテストしてましたが, 7, 8 回書き直したので自分の実装力の NASA を感じる
でも 14:00 くらいに実装出来たのでベンチ通したらスコアが 600 点 -> 3000 ~ 5000 点くらいになってテンションが上がった
get_event 周りの所感
~競技終了まで
これ終わった後は特に改善できそうなところがよくわからなかったので終わり
- 他の 2 人が改善していたっぽい
- データベースの reservations に event_id, user_id, sheet_id の外部キー登録すると改善するのかなーと思ったけどパッとうまくいかなかったし, データベース変更しちゃったらどうしようという不安に襲われたのでやめた
最終的には 8000 点くらいだったっぽく, 予選落ち
- 残念
まとめ
UNDERTALE はいいぞ!
undertale.jp
(PVだけ見るとオススメしづらそうなのやめろ)
TypeScript を使ってオセロを実装してみた(2)
やったこと
前の続きです。
mayokoex.hatenablog.com
今回は通信対戦できるようにしました。
また, せっかくなので, それを web 公開しました。こちらから遊べます。(出来がアですが)
- 「1」と書いてあるところで番号を選んで部屋を選択し, Name と書いてあるところに名前を入れると, 指定した番号の部屋に入れます。
- 部屋に二人入ると対戦が始まります。
方針
今回は, nodejs と socket.io を使いました。
nodejs はサーバーを立てるときによく使うっぽくて, また, socket.io はチャットをするときとかによく使われるっぽいです。
(実際, socket.io でググるといろんな人がチャットツールを作っています)
で, 公開するために heroku というのを使いました。
jp.heroku.com
苦労したこと
実装はかなり簡単だったのですが(さすが socket.io), 環境構築系ですごく苦労しました。
npm
まず, javascript は外部ライブラリをインストールしないといけないです。
で, このインストールは gcc みたいに一回インストールしたらもうやらなくていいみたいなものではなく, 作りたいアプリごとにインストールするものです(node_modules というディレクトリに全部入ります)。
このインストールは, npm install [package 名] --save とやると出来ます。
また, node_modules に入るのは javascript のコードなので, typescript からすると型とかそもそもインストールしたのが何かわからない, という状況なので, 型情報を教える必要があります。
このインストールは npm install @types/[package名] --save とやると出来ます。
これらのことを, たたもさんに教えていただきました。ありがとうございました!
はい。たとえば import なんとか from 'foo';とやると、./node_modules/fooディレクトリを見に行くのでfooというライブラリを読み込むことができます(実際には./node_modules/foo/index.js等が読み込まれます)。 npm installはこのnode_modulesディレクトリに外部ライブラリをダウンロードする操作です
— たたもさん@がんばらない (@__tatamo__) 2018年6月23日
ここら辺のことを把握すると, このページで書かれていることのコマンドの意味が分かりやすいです。
ics.media
browserify
今回の構成では,
- typescript コードを書く
- javascript コードにコンパイルされる
という流れで javascript コードが生成されますが, main.js の方は, コンパイルしたコードを動かそうとしても「require ってなんだよ」みたいなことを言われて実行することが出来ません(require が nodejs 専用の機能で普通に js を動かす分には利用できないとかなんとか)。
今回は socketio を使う際に require がコンパイル後に使われていて, そこでエラーになりました。
この問題は, browserify というのを使うと解決しました。
ただこれをやると行数が 500 行くらいから 8000 行くらいになるのでこれで正しいのかと若干心配になります…
express パッケージの追加
- 結局オセロプレイ画面になる index.html を開いてほしかったのですが, それをやるときに app.js 内で
const app = express(); const server = http.createServer(app); app.use(express.static(__dirname + '/public')); app.get('/', (request, response) => { response.sendFile(__dirname + '/index.html'); });
とやると出来ました。
ただし, フォルダ構成として, /public/ に index.html, style.css, main.js が置いてあります。
app.use で「public にあるファイル使うぜー」って言って, app.get で, 「アクセスされたら index.html 開くぜー」と言っていそう。
ポート番号
上のコードのあとに,
server.listen(process.env.PORT || 8000);
をやるとアクセスしたときにちゃんとページを開いてくれます。
process.env.PORT ってお前どっから出てきたんだ。
ローカルで実験するときは localhost:8000 とかでやってたので出来てるんですが, heroku でやるときはポート番号が違うっぽいです(どこで決めてるのかは知らないですが)。
node_modules は git の管理下に置かない
node_modules を git の管理下に置いておくと, push したときに reject されます。
.gitignore で node_modules を消しておく必要があります。
まとめ
web 難しい…
ホモグラフィ変換
はじめに
OpenCV でホモグラフィ変換すると遅いので OpenGL でホモグラフィ変換する, というのはよくある流れだと思うのですが, 最初に OpenCV でホモグラフィ変換用の行列 H を求めていると, OpenGL 用の座標系 に変換するのがめんどくさいです。
(ちなみに, OpenCV でホモグラフィ変換する場合には, warpPerspective 関数を使います)
ここで, H はなんかの座標系から画像座標系へのホモグラフィ変換行列だとします。この画像座標系の画像の高さを h, 横の長さを w とします。
すると,
- (0, 0) から (-1, -1)
- (0, h) から (-1, 1)
- (w, h) から (1, 1)
- (w, 0) から (1, -1)
のホモグラフィ変換行列 H' がわかれば, なんかの座標系から OpenGL へのホモグラフィ変換行列は, H' * H として記述できます。
4 点と 4 点の間を結ぶ平面間の変換はホモグラフィ変換でできるのですが, 直感的に思いつく変換だとうまくいかなかったので, 少し真面目に計算して H' がどうなるのかを調べたというのがこの記事です。
結果
まとめ
OpenGL はもうちょっと気軽に使えるようにして。
TypeScript を使ってオセロを実装してみた
オセロです。
index.html, style.css, main.ts を同じフォルダに入れ, main.ts をコンパイルして main.js を作って, index.html をブラウザで開くと一人二役のオセロで遊ぶことが出来ます。
github.com
追記:こちらから遊べます
オセロ
通信対戦までやりたいので, まだ途中ですがある程度まとまったのでとりあえず公開です。
通信対戦は typing war みたいなのかっこいいので真似出来ればしたいです。
Typing War | traP
微妙にオブジェクト指向を意識しました。
クラス間の関係みたいのをメモした図はこちらです(オブジェクト指向の考えかたわからん)。
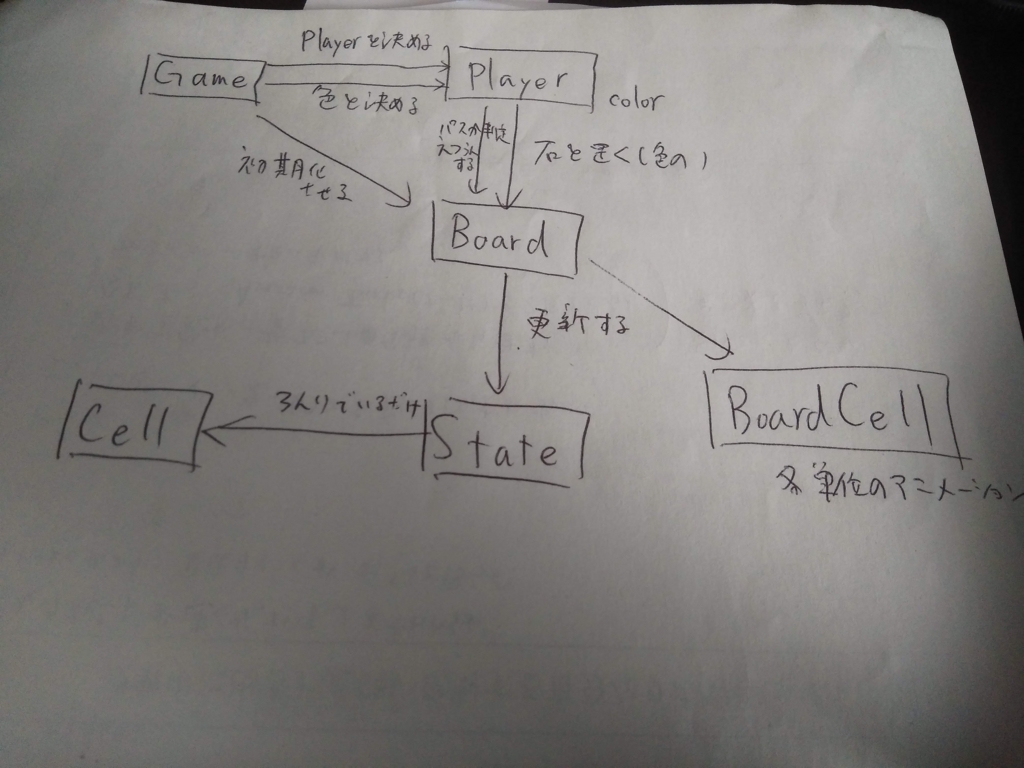
途中でめんどくさくなって if (this.board.state.board[i][j].get() === Cell.white) とか書いてあるのは御愛嬌です。
本当は Board クラスに get(i, j) っていうのを入れておいたほうが良さそうです。
今一番気になってるのは, createElement の型をどう書くのってところです(無理なのかな?)。
this.elem = createElement("div");
とか書くのですが, クラスのメンバとして elem を入れてないとダメなのでその時に elem: type みたいな感じで書かないとダメですが, type が分からないので人生終了です。
一時変数だったら const elem = createElement("div") とか書けば賢い visual studio code 君がインテリセンスを発動してくれるのですが, クラスのメンバだとダメです。
追記:しょラーさんに教えていただきました。ありがとうございます!
createElementをマウスホバーすると型が出てきませんか? あとJavaScriptで作ったならgh-pagesで公開するとみんなが遊べるので良い感じです
— しょラー (@shora_kujira16) June 17, 2018